Análisis Cinemático de Mecanismos

Definición de mecanismo

Según la Real Academia Española (RAE), un mecanismo es el conjunto de las partes de una máquina en su disposición adecuada. También se define como la combinación de piezas necesarias para realizar un trabajo o función dentro de un artefacto. Esta definición resalta la importancia de la organización y el propósito funcional de los elementos que conforman un sistema mecánico.

Más allá de su definición general, en este artículo abordaremos el concepto de mecanismo desde el enfoque del análisis cinemático. Aquí lo analizaremos mediante la identificación de eslabones, pares cinemáticos y la determinación del grado de libertad de un sistema mecánico, utilizando herramientas como la ecuación de Gruebler y ejemplos visuales para su comprensión.

Según Joseph Edward Shigley, en su libro Theory of Machines and Mechanisms, un mecanismo es:

“A system of rigid bodies connected by joints to transmit motion and force”
(Un sistema de cuerpos rígidos conectados por uniones para transmitir movimiento y fuerza).

Conceptos de Mecanismos

1. Mecanismos, Máquinas y Estructuras

Es importante diferenciar estos tres términos:

• Mecanismo: Conjunto de eslabones con movimiento relativo que transforma o transmite el movimiento sin necesariamente realizar trabajo útil.
• Máquina: Mecanismo diseñado para realizar trabajo útil mediante la conversión de energía.
• Estructura: Sistema de eslabones sin movimiento relativo, utilizado para soportar cargas sin transformar movimiento.

Ejemplos:

• Un limpiaparabrisas es un mecanismo de cuatro barras, ya que transforma el movimiento rotatorio del motor en un movimiento alternativo de las aspas sin realizar trabajo útil directo.
• Un motor de combustión interna es una máquina, ya que convierte energía térmica en energía mecánica para mover un vehículo.
• Un puente es una estructura, pues sus elementos no tienen movimiento relativo entre sí y solo soportan cargas.

Esta distinción deja claro que un mecanismo es simplemente un sistema que transforma el movimiento, mientras que una máquina es un mecanismo o un conjunto de ellos diseñados para realizar trabajo útil.

2. Máquinas Simples

Son dispositivos mecánicos básicos que transforman una fuerza para facilitar el trabajo sin alterar su naturaleza. Generalmente están formadas por un solo mecanismo.

Ejemplos de máquinas simples:

• Palanca: Transmite fuerza y movimiento rotatorio alrededor de un punto de apoyo.
• Plano inclinado: Reduce el esfuerzo necesario para elevar una carga.
• Tornillo: Convierte movimiento rotatorio en lineal, amplificando la fuerza aplicada.
• Polea: Permite cambiar la dirección de una fuerza aplicada para levantar cargas.
• Cuña: Convierte una fuerza aplicada en una separación de materiales.
• Rueda y eje: Facilita el movimiento reduciendo la fricción.

3. Máquinas Compuestas

Son sistemas mecánicos que combinan dos o más máquinas simples para realizar un trabajo más complejo. Están formadas por múltiples mecanismos interconectados.

Ejemplos de máquinas compuestas:

• Automóvil: Integra mecanismos como el motor, la transmisión y el sistema de dirección.
• Bicicleta: Utiliza ruedas, engranajes, cadenas y pedales para transformar la energía del ciclista en movimiento.
• Grúa: Combina poleas, cables y sistemas hidráulicos para levantar y mover cargas pesadas.

Esta clasificación es clave para entender cómo se combinan los mecanismos en sistemas más avanzados, como robots, herramientas industriales y maquinaria pesada.

4. Eslabón

Un eslabón es cada cuerpo rígido dentro de un mecanismo. Puede ser fijo o móvil y se conecta con otros eslabones para formar una cadena cinemática.

Ejemplo:
• En un motor de combustión interna, la biela y el cigüeñal son eslabones móviles.

5. Pares Cinemáticos

Los pares cinemáticos son las uniones entre los eslabones que permiten el movimiento relativo entre ellos. Se clasifican en:

• Pares de baja movilidad (pares inferiores): Superficies en contacto amplio, como una bisagra.
• Pares de alta movilidad (pares superiores): Contacto en un punto o línea, como un rodamiento.

6. Grados de Libertad (GDL) Ecuación de Gruebler:

Los grados de libertad indican cuántos movimientos independientes puede realizar un mecanismo. Se calculan con la Ecuación de Gruebler:

GDL=3(n−1)−2j−h

Donde:
n = número de eslabones
j = número de pares cinemáticos de revolución
h = número de pares de alta movilidad

Ahora si ya obtuviste el resultado del cálculo de GDL, es importante comprender qué significa en términos de movilidad del mecanismo. El número obtenido indica si el sistema tiene libertad de movimiento, está restringido o si es completamente inmóvil.

El resultado obtenido debe interpretarse con base en los siguientes criterios:

1. Si GDL= 1 o un número positivo bajo (como 2 o 3):

• El mecanismo es móvil y se necesita una cantidad específica de entradas (movimientos controlados) para operar correctamente.
• Ejemplo: Un mecanismo de cuatro barras tiene GDL=1GDL = 1GDL=1, lo que significa que su movimiento queda determinado por una única entrada, como una manivela.

2. Si GDL = 0

• El sistema es una estructura estática, lo que significa que no tiene movilidad.
• Ejemplo: Un puente o un marco rígido no tienen movimiento relativo entre sus partes.

3. Si GDL < 0 (valor negativo):

• El sistema es una estructura hiperestática o está sobrerrestricto, lo que indica que tiene más restricciones de las necesarias y no puede moverse.
• Ejemplo: Un mecanismo donde los eslabones están sobredimensionados o se agregaron restricciones innecesarias.

4. Si GDL>1:

• El mecanismo tiene más de un grado de libertad, lo que significa que necesita más de una entrada independiente para su movimiento completo.
• Ejemplo: Un robot paralelo con GDL=3GDL = 3GDL=3 puede necesitar tres motores para controlar sus movimientos en el espacio.

Pasos para aplicar la ecuación de Gruebler

1.-Identificar y contar los eslabones del mecanismo (n):

• Incluye tanto los eslabones móviles como el eslabón fijo.

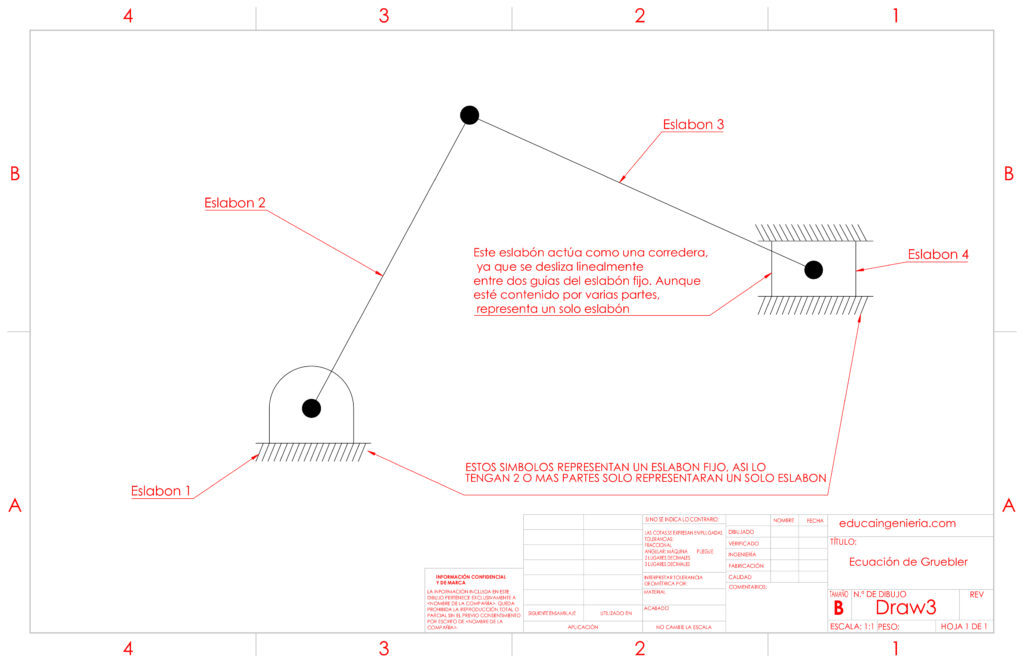
Contar los pares cinemáticos de un grado de libertad:

• Como rotacionales (revolute joints) o prismáticos de deslizamiento lineal (prismatic joints).
• En este mecanismo solo se consideran pares de un grado de libertad, por lo que h = 0.
• La ecuación básica para contar los pares cinemáticos es: n−1=j

donde:

• n es el número de eslabones conectados en un mismo punto (o nodo).
• j es el número de pares cinemáticos generados por esa conexión.

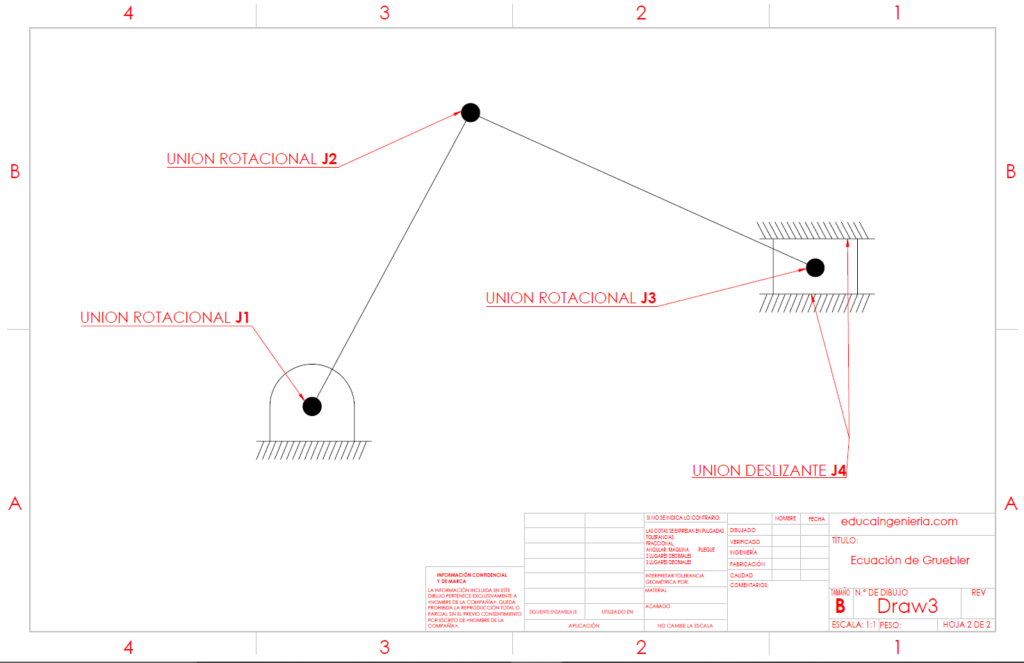
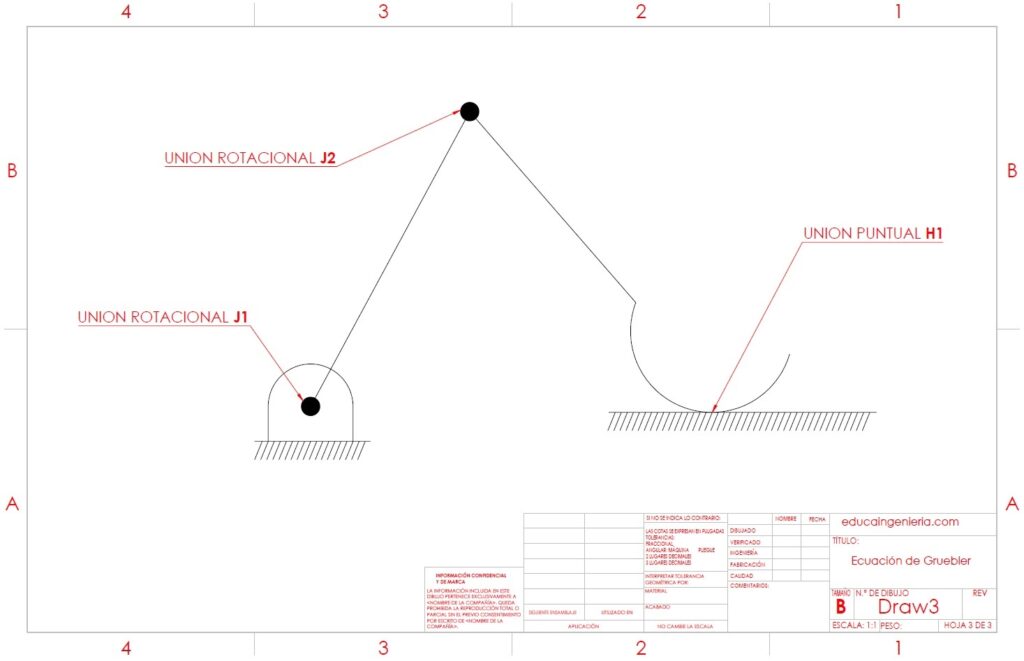
Veamos a continuación el análisis del siguiente mecanismo para identificar sus eslabones y pares cinemáticos

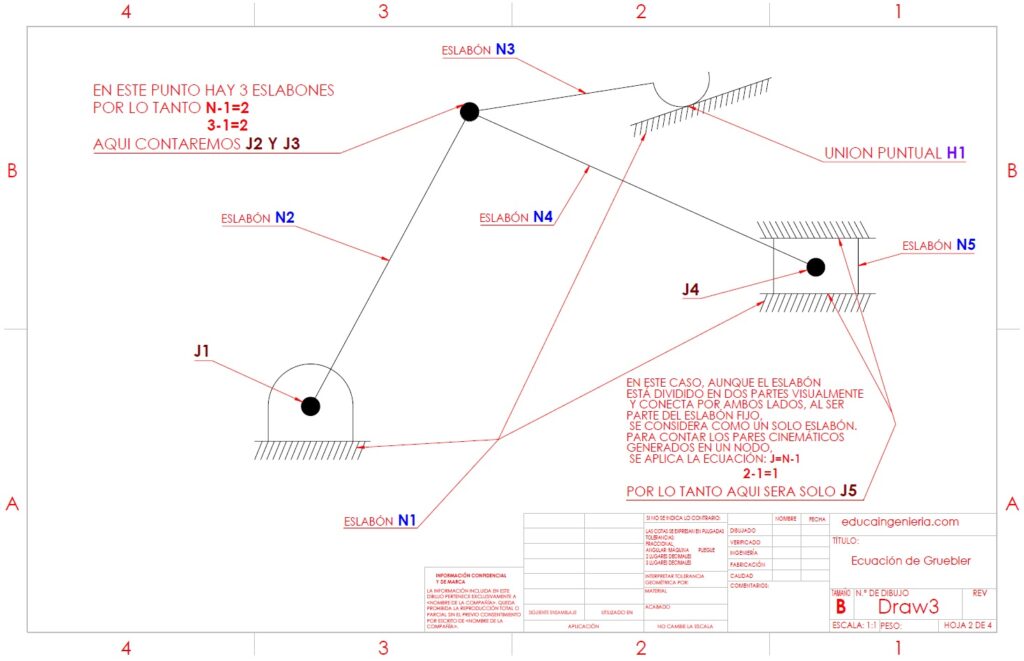
Ya se tiene el conteo de los elementos necesarios para aplicar la ecuación de Gruebler:

• n=5
• j=5
• h=1

Realizamos la sustitución en la ecuación de Gruebler:

• GDL=3(n−1)−2j−h

Sustituyendo los valores y resolviendo:

• GDL=3(5−1)−2(5)−1
• GDL=3(4)−10−1
• GDL=12−10−1=1

Por lo tanto, el mecanismo tiene 1 grado de libertad, lo que significa que todo su movimiento puede ser controlado mediante una sola entrada

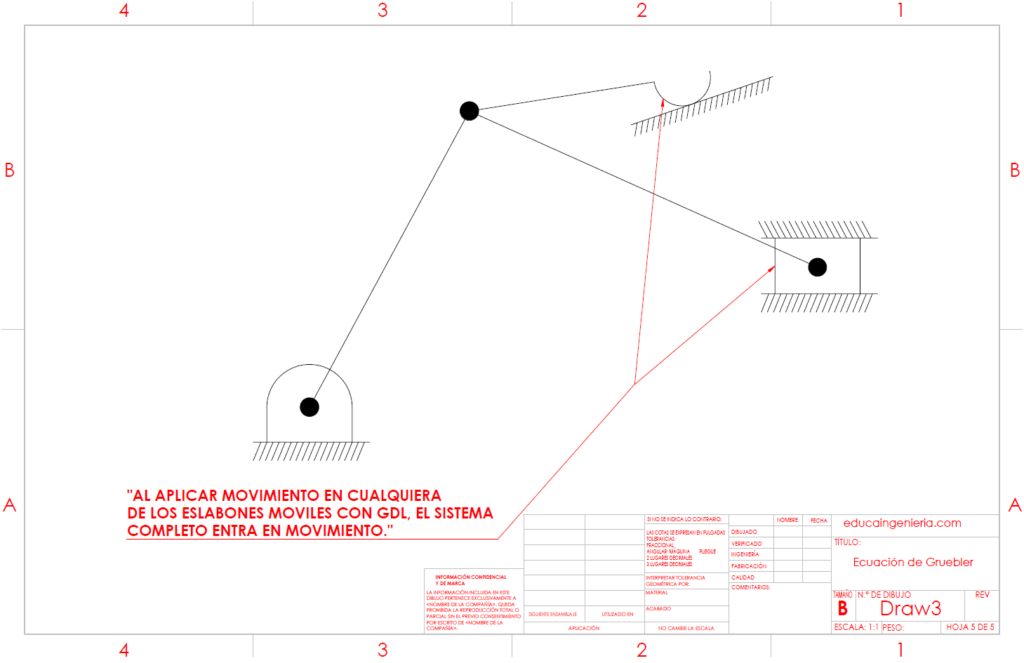
Conclusión:

El análisis cinemático de mecanismos es una herramienta fundamental para comprender el comportamiento y la movilidad de sistemas mecánicos. A través del conteo de eslabones y pares cinemáticos, y la aplicación de ecuaciones como la de Gruebler, es posible determinar los grados de libertad de un mecanismo y predecir cómo se moverá bajo ciertas condiciones. Este tipo de análisis no solo permite diseñar sistemas más eficientes, sino también identificar posibles limitaciones o redundancias en su estructura. La correcta interpretación de uniones, movimientos y elementos interconectados es clave para el desarrollo de soluciones mecánicas funcionales y controladas.